![]() Geometrische en stereometrische vormen
Geometrische en stereometrische vormen
 |
Je kunt alle denkbare vormen ruwweg verdelen in twee soorten: de geometrische en de helemaal niet geometrische vormen.
Geometrische vormen zijn alle vormen, die je met behulp van passer en liniaal kunt construeren, zoals het vierkant (de rechthoek), de driehoek en de cirkel. Geometrische vormen zijn vooral in de architectuur altijd veel toegepast en dat is heel verklaarbaar: ten eerste zijn ze goed berekenbaar en ten tweede moeten ruimtes en verdiepingen op elkaar aansluiten en dat gaat nu eenmaal het gemakkelijkst met geometrische vormen.
Geometrische vormen zijn berekende en controleerbare vormen en daarom werden ze door deze architecten verkozen boven niet-geometrische; bij een goed evenwicht tussen de praktische functies van een gebouw en de toegepaste (geometrische) vormen moest vanzelf een schoonheid ontstaan, die geen versieringen meer nodig had behalve eventueel kleur.

Sommige gebruiksvoorwerpen hebben al sinds mensenheugenis voornamelijk geometrische vormen: tafels b.v. (vierkant, rechthoekig of rond) en borden (rond). Dat heeft vaak te maken met de wijze van maken en met het soort gebruik dat ervan gemaakt wordt. Maar over het algemeen geldt bij gebruiksvoorwerpen altijd meer dan bij architectuur dat de vorm precies de functie volgt en dientengevolge niet-geometrisch is.
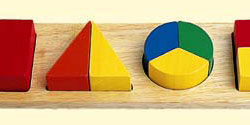
De afbeeldingen hierboven laten enkele bijzondere geometrische vormen zien: ze zijn niet plat, maar ruimtelijk en daarom noemen we ze stereometrisch. Door erop te klikken worden ze vergroot en gaan ze ronddraaien. Probeer het aantal vlakken uit te rekenen!
![]() De
uitslag
De
uitslag
We verstaan onder dit begrip het volgende: een twee-dimensionale tekening van een drie-dimensionale vorm, waarbij alle vlakken aan elkaar vast zitten en door snijden, vouwen, ritsen of rillen een ruimtelijke vorm oplevert.
Rillen doe je met de stompe punt van een schaar, snijden en ritsen met een stanleymes. Je snijdt bij ritsen dan niet meer dan 1/3 van de kartondikte in.
De uitslag van een twintigvlak
15-01-2005 vaklokaal bevo