|
Tellen is vertellen |
|
| Vanaf de oudheid tot enkele eeuwen na de uitvinding van de boekdrukkunst in de vijftiende eeuw was het grootste deel van de bevolking analfabeet. Zij kon niet lezen of schrijven, maar de meesten van hen konden wel tellen, waarbij van-ouds de vijf vingers van de hand als hulpmiddel gebruikt werden. Daarmee ontstond een taal van getallen, die in vele Europese talen geleid heeft tot het werkwoord 'vertellen', waarin de stam 'tellen' is waar te nemen: raconter erzšhlen, to tell, contar, raccontare. Al in het oude Egypte is een symbolische taal ontstaan van getallen, die een andere betekenis hebben dan alleen het aangeven van een hoeveelheid. | |
| Het schijnt dat de Egyptenaren de natuur van het heelal met een rechthoekige driehoek vergeleken hebben. Daarvan vertegenwoordigde de opstaande zijde het getal drie, de liggende zijde het getal vier en de schuine zijde het getal vijf. Men moet de opstaande zijde als symbool van het mannelijke beschouwen (Osiris), de basis als symbool van het vrouwelijke (Isis) en de schuine zijde als datgene wat uit de vereniging van beide andere geboren wordt, het kind (Horus).' | |
|
Moeilijker wordt de herkenning voor de hedendaagse mens van de symbolen, die de bouwers van de gotische kathedralen hebben gebruikt om dezelfde grondbeginselen tot uiting te brengen in getallen en de daaruit voortvloeiende geometrische figuren. Door ons worden getallen voornamelijk als rekeneenheden toegepast en onze kinderen weten wel wat even en oneven getallen zijn, maar een diepere betekenis daarvan ontbreekt. Toch is de cultuur van de Middeleeuwen voor een belangrijk deel gebaseerd op getallen, die voor de analfabetische mens boodschappen inhielden, die zijn tekortkomingen op het gebied van het lezen en schrijven enigzinds compenseerden. Daarvoor waren de in de tiende eeuw ingevoerde Arabische cijfers niet van toepassing, maar al sedert de Egyptische oudheid was er het cijfer-schrift met verticale streepjes, waarvan wij vandaag nog de overblijfselen kennen als 'Romeinse cijfers'. |
|
|
In dat systeem was de eenheid als ťťn verticale streep | aangegeven, waarin wij ook nu nog de oorsprong van het getal 1 herkennen. Door de deling van de 1 in twee verticale streepjes || ontstond het getal 2 uit het getal 1. Hierbij zien we al direct dat het huidige Arabische cijfer 2 geen enkele band meer heeft met het getal || uit de oudheid. Om het getal 2 te kunnen 'ontcijferen', moet men echter de vorm van dat getal door een leerproces uit het hoofd kennen. De analfabeet, die wel kan tellen, maar niet kan lezen, kan de || wel degelijk 'herkennen'. Zo ontstond dus meer dan vierduizend jaar geleden een getallenschrift, dat tot vandaag op de wijzerplaten van de klokken op kerktorens voortleeft, maar dat met name in de Middeleeuwen de boodschap van de kathedraalbouwers op de massa overbracht. Daarbij ging men verder dan alleen het aangeven van aantallen, maar gebruikte men ook in vele gevallen de 'geometrische' vormen van de getallen boven de | en de ||. Van deze beide eerste getallen is namelijk geen kenmerkende figuur te maken, wat wel het geval is met de waarden hoger dan ||. |
|
|
Zo is al in het oude Egypte het getal ||| synoniem met de gelijkzijdige driehoek en werd voor het getal |||| ook het vierkant toegepast. Daarbij wist de bevolking, dat de driehoek de mannelijke godheid Osiris symboliseerde en het vierkant de godin Isis. In de geometrische uitwerking van hoofdopzet en details van de gotische kathedralen waren de driehoek en het vierkant de voornaamste basisfiguren. Zij hebben gedurende een aantal eeuwen geleid tot een zogenaamd 'ad triangulum'- en een 'ad quadratum' - systeem, het eerste gebaseerd op de driehoek en het laatste op het vierkant. Daarin vertolkte de driehoek het spirituele en het vierkant het materiŽle beginsel: de uitwerking van het eerste vindt men hoofdzakelijk aan de zuidelijke gevel en die van het laatste aan de westelijke gevel. |
|
|
|
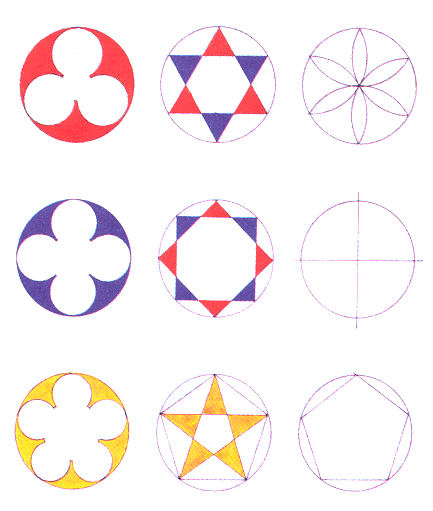
In de bovenstaande tekening zijn de grondslagen van de geometrie volgens het 'ad triangulum'-systeem (de triangulatuur bovenste rij) en het 'ad quadratum'-systeem (de kwadratuur middelste rij) aangegeven. In de onderste rij is de regelmatige vijfhoek afgebeeld, met de daarvan afgeleide vijfpuntige ster en de vijflobbige figuur.
|
|
Het geometrisch construeren van de driehoek en het vierkant was in de Middeleeuwen bij de werklieden in het bouwvak algemeen bekend. De kennis van de constructie van de regelmatige vijfhoek was echter voorbehouden aan de bouwmeester en zijn naaste medewerkers.Uit de constructie van de driehoek en het vierkant volgt op eenvoudige wijze die van de zeshoek en de achthoek, die tot dezelfde 'families' behoren. Hetzelfde geldt voor de vijfhoek en de daaruit afgeleide tienhoek. De regelmatige zevenhoek, de negenhoek, elfhoek, dertienhoek, enz. zijn niet volgens de beginselen van de geometrie met passer en liniaal te construeren. Zij komen bij de middeleeuwse kathedralen dan ook niet voor. De kleur rood duidt op het actieve, blauw op het passieve beginsel en het goudgeel op de svnthese van beide andere kleuren. |
|
 |
Het noordoostelijke roosvenster van
de kathedraal van Amiens toont duidelijk
de vijjhoek als belangrijkste geometrische figuur
in de vorm van een vijfpuntige ster. Die ster ontstaat
als het ware uit de driehoeken en vierkanten aan de rand.
Geheel onderaan wordt het raam gedragen door vijf in drieŽn gedeelde boogvensters. Van de 15 daardoor ontstane smallere vensters zijn, van links afgeteld, het vijfde, het elfde en het vijftiende venster dicht. Daardoor ontstaat geheel links (aan de westzijde) een groep van vier glas-in-loodramen, geheel rechts (aan de oostzijde) een groep van drie en in het midden een groep van vijf ramen. Deze demonstratie van de 3-4-5-symboliek kan geen toeval zijn. |
|
02-17-2018 CKV-2 Geraadpleegde bron: M Gout Symboliek in kathedralenbouw Den Haag 2001 |
|