|
Gebouwde muziek |
||
| Een architect moest de 'Kunsten' hebben gestudeerd en met name die van het quadrivium goed beheersen. Wat Nicolaas van Cusa in zijn belangrijkste werk 'De docta ignorantia' hierover schreef, was ook de opvatting van de geleerden in Chartres: 'God heeft bij de schepping van de wereld gebruik gemaakt van de aritmetica, de geometrie, de muziek en de astronomie, kunsten die wij eveneens toepassen als we de proportionele verhoudingen van voorwerpen, elementen en bewegingen onderzoeken.' | ||
 De
docta ignorantia Titelblad. De
docta ignorantia Titelblad. |
||
| Volgens
welke methode ging de architect te werk? Van welke techniek maakte hij
gebruik om de principes van de harmonie te vertalen naar werkelijke
gebouwen?
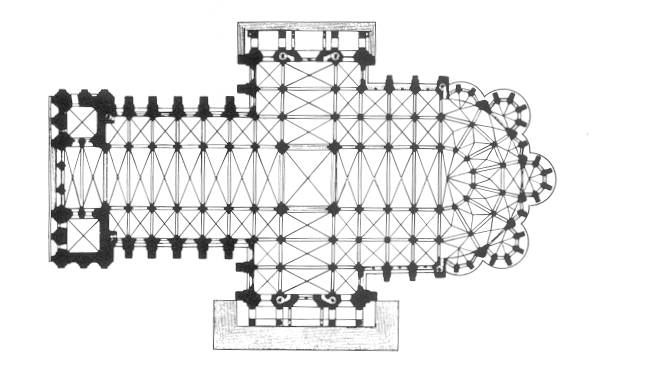
In een onderzoek is men erin geslaagd om, uitgaande van de maatverhoudingen van de plattegrond, de bouwgeheimen van de bouwmeesters van de kathedraal van Chartres bloot te leggen. Anders dan bij andere kathedralen is in Chartres de viering niet vierkant, maar rechthoekig van vorm, het dwarsschip is dus smaller dan het schip. De breedte werd bepaald op 50 voet Š 32,8 cm (14,4 m, steeds van het middelpunt van de zuilen gemeten).
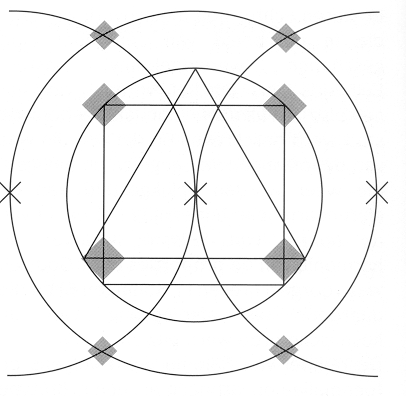
Deze maat werd overgenomen van het voorgaande romaanse gebouw. Alle overige maten zijn daarvan afgeleid. De lengte van de korte zijde bedraagt 13,99 m. Het verschil van 2,41 m komt precies overeen met de dikte van de gekantonneerde pijlers (inclusief colonnetten) en met de breedte van de vensters van de benedenverdieping! De precieze plaats van de vieringszuil is bepaald door de volmaaktste geometrische figuren, de cirkel en de daarin getekende gelijkzijdige driehoek (volgens Plato de 'mooiste driehoek'), zoals het schema laat zien: |
||
|
|
Constructieschema, waaruit volgens de berekeningen de plaats van de vieringspijlers en die van de pijlers van het koor en het schip (grijs) voortvloeien. Uit de maatverhoudingen van de zo ontstane vieringsrechthoek kunnen de verdere maten van de kathedraal worden afgeleid. | |
| De bouwmeester tekende om het centrum van de viering een cirkel met als straal de langste zijde (let wel: de van het romaanse gebouw overgenomen afstand van 50 voet = de breedte van het koor). Daaruit leidde hij de plaats van de meest oostelijke pijler van het schip en van de eerste koorpijler af. Daarmee is de maat van alle overige traveeŽn van het schip en het koor bepaald. Met behulp van een heel systeem van dergelijke cirkels met dezelfde straal kon de architect alle overige ruimten uitzetten. Ook de plaats voor het labyrint, de breedte van het schip, de plaats van het altaar, de vorm van de apsis en de straalkapellen werden zo berekend. | ||
| Wat
een prachtig helder en goed doordacht plan! Men kan zich alleen maar
verbazen over het genie van de onbekende architect van Chartres, die
deze stelsels van cirkels en lijnen, krommen en rechten, kardinale
punten en symmetrische afstanden heeft bedacht en bij wie men bij het
reconstrueren van zijn plannen een beetje 'over de schouder kan kijken'.
De heldere, overtuigende reconstructie van de door de architect gehandhaafde praktische geometrie zou de vele pogingen tot symbolische geometrie geheel overbodig maken, die door het intekenen van allerlei vijf-, zeven- en twaalfpuntige sterren of andere ingewikkelde vormen in de plattegrond op hun best willekeurig zijn en nauwelijks iets bijdragen tot het begrip van de werkelijke opbouw van de plattegrond - of van de kathedraal zelf. |
||
| Bovendien
is overduidelijk te zien, en hieruit blijkt maar weer eens de ware
symboliek van Chartres, dat het schip uit zeven traveeŽn bestaat die
door het labyrint in twee delen van drie en vier worden verdeeld. Er
zijn ook zeven straalkapellen - drie grote en vier kleine. Men kan hier
aan de drie (trivium) en de vier (quadrivium) Vrije Kunsten denken, maar
ook aan de drie 'goddelijke' en de vier hoofddeugden - beide zijn in de
portalen afgebeeld.
Toch kennen we, in tegenstelling tot de kathedralen van Reims en Parijs, noch de naam van de architect van de kathedraal van Chartres, noch iets naders over zijn leven of afkomst. We kunnen echter uit zijn gebouw zeker concluderen dat hij tot de geniaalste architecten van zijn tijd kon worden gerekend. Niet in de laatste plaats aan de maatverhoudingen zien we dat hij zich de kennis van die tijd over de verhoudingen en hun toepassing geheel eigen had gemaakt. Wat hij heeft geschapen, is dan ook echt 'gebouwde muziek'!
|
||